Diese Seite funktioniert nur mit Javascript.
Allokationsverlust durch eine Steuer4.1.5.1.3 Negative SteuernMengen- und Preiskontrollen
egative Steuern? Das hört sich erst einmal komisch an! Aber es gibt sie tatsächlich. Sie haben nur einen anderen Namen:
Subventionen kommen wie Steuern in unterschiedlichsten Ausprägungen daher. Tatsächlich gibt es eine negative Steuer, die auch so heißt: die negative Einkommensteuer. Sie ist ein vergleichsweise modernes Instrument am Arbeitsmarkt, Arbeitsanreize für Geringverdiener zu fördern, indem sie geringe Einkommen subventioniert und erst ab einer festgelegten Einkommensschwelle zu einer "richtigen Steuer" wird. Die negative Einkommenssteuer geht sozusagen fließend mit steigendem Einkommen von einer Subvention in eine Steuer über.
Wir beschränken uns hier aber auf ein einfacheres Beispiel, in dem der Staat einen fixen Subventionsbetrag pro Gütereinheit zahlt. Da wir unsere Erkenntnisse über die Wirkungen einer Mengensteuer nahezu unverändert übernehmen können, verpacken wir die Betrachtung in einer Übungsaufgabe:
Gehen Sie im Folgenden von vollkommenen Konkurrenzmärkten aus.
Nachdem die Nachfrage auf dem Markt für Gut X – eine Schlüsselindustrie in dem betrachteten Land – eingebrochen ist, lassen sich Angebot und Nachfrage beschreiben durch
$$x_N = 100 - p $$ $$x_A =-100 + 4p $$Die X-Produzenten drohen Massenentlassungen an, woraufhin die Regierung ein Sofortprogramm beschließt: In der nächsten Periode erhält jeder Käufer eines neu produzierten X eine Subvention $s$ in Höhe von 10 Geldeinheiten. Die Käufer zahlen also statt $p$ nur noch $(p-s)$ für ein neues $x$, sodass sich die Nachfragefunktion ändert zu
$$x_N = 100 - (p-s) $$Ja, es ist tatsächlich so einfach, die Subvention in das Modell einzubauen: Die Nachfrager zahlen nach Einführung der Subvention nicht mehr $p$, sondern nur noch $(p-s)$. Damit fällt der Preis $p$, den die Anbieter erzielen, genau um den Subventionsbetrag $s$ höher aus als der Preis, den die Käufer netto entrichten: $(p-s)$. Denken Sie einmal darüber nach, wie man eine Subventionierung der Anbieter in das Modell hätte implementieren können.
a) Bestimmen Sie das Marktgleichgewicht in der Ausgangssituation und stellen Sie es im Diagramm dar.
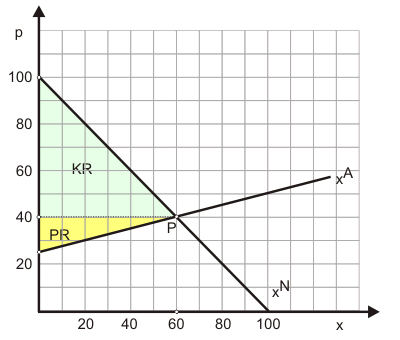
Das Gleichgewicht P lässt sich mit einer maßstabsgetreuen Zeichnung leicht bei $p^*=40$ und $x^*=60$ ermitteln.
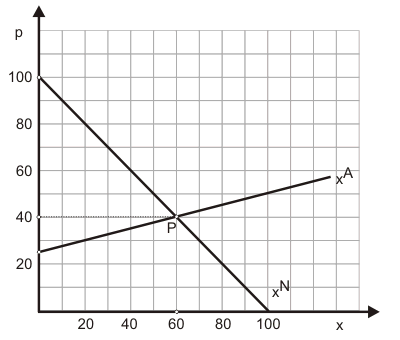
b) Berechnen Sie die Veränderung der Menge, die durch die Subvention erreicht wird.
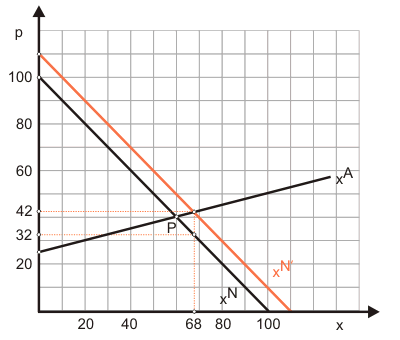
Dazu ersetzen wir die ursprüngliche einfach durch die neue Nachfragefunktion und für $s$ den Subventionsbetrag 10 ein. Dann bringen wir Angebot und Nachfrage zum Ausgleich:
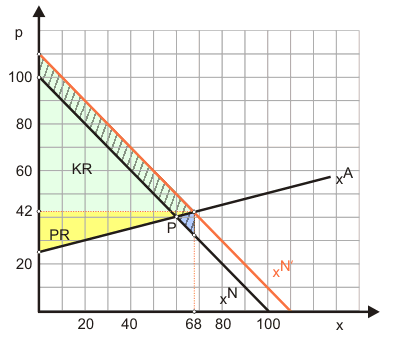
$$ 100 - (p - s) = -100 + 4p $$ $$ 100 - (p - 10) = -100 + 4p $$ $$ 100 - p + 10= -100 + 4p $$ $$ 210 = 5p $$ $$ p^* = 42 $$ $$ x^* = 68 $$Die orangefarbene Funktion xN' zeigt die subventionierte Nachfrage. Die Subvention löst eine Nachfragesteigerung aus, was den Preis auf 42 steigen lässt. Netto (Preis minus Subvention) kostet die Konsumenten ein Stück aber nur noch 32.
c) Bestimmen Sie die Renten vor und nach der Subvention.
Ohne Subvention berechnet man in der Ausgangssitution die Konsumentenrente KR zu 1800 und die Produzentenrente PR zu 450. Die Gesamtrente beträgt also 2250 (s. Abbildung 3). Die Subvention lässt die Konsumentenrente auf 2312 und die Produzentenrente auf 578 steigen. Der Anstieg der Gesamtrente bleibt mit 640 aber hinter den Kosten der Subvention in Höhe von 680 zurück. Die Differenz ist der blau dargestellte Allokationsverlust (s. Diagramm in Abbildung 3).
d) Der Wirtschaftsminister erklärt vor der versammelten Presse auf die Frage, ob es denn richtig sei, mit Steuergeldern die x-Industrie zu subventionieren: "Ich und die Kanzlerin, äh, die Kanzlerin und ich, wir sind uns hier einig. Wir tun was für die Verbraucher. Die x-Industrie erhält keinen Heller. Die Subvention geht direkt an die Verbraucher und wird von den Finanzämtern bei Vorlage des Kaufbelegs ausgezahlt. Durch unser Sofortprogramm spart jeder x-Käufer 10 Euro."
Das ist so nicht richtig. Zwar sparen die Konsumenten im Zahlenbeispiel ordentlich, aber der Preis für ein x sinkt nicht um den vollen Subventionsbetrag in Höhe von 10, sondern nur um 8. Auch die x-Industrie profitiert. Dass ihr Vorteil nicht so groß ausfällt wie der der Konsumenten, liegt an der relativ hohen Elastizität der Angebotsfunktion.
e) Wie hoch müsste Subvention je $x$ an die Produzenten sein, sodass ein gleich hoher Effekt ausgelöst wird, wie unter b) berechnet?
Die Subvention müsste natürlich ebenfalls 10 pro x betragen. Anstelle der Nachfragefunktion würde sich die Angebotsfunktion verschieben. Alle Wirkungen wären identisch.
Die Umweltprämie, die die Bundesregierung zur Bekämpfung der Rezession im Januar 2009 beschlossen hat, liefert übrigens ein praktisches Beispiel für die in der Übungsaufgabe behandelte Problematik. Sie ist eine "Subvention pro Stück", Bemessungsgrundlage ist also die Menge. Im Unterschied zu vielen anderen Subventionen hat die Regierung bei der Umweltprämie etwas richtig gemacht: Von vornherein war klar, dass mit der Subvention Schluss ist, wenn die Finanzmittel von 1,5 Mrd. Euro verbraucht sind. Denn bei allen theoretischen Gemeinsamkeiten von Steuern und Subventionen gibt es doch einen ganz entscheidenden Unterschied: Die Reduzierung oder Abschaffung einer Steuer ist politisch viel einfacher durchzusetzen als die Reduzierung oder Abschaffung einer Subvention.